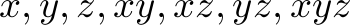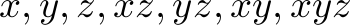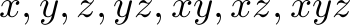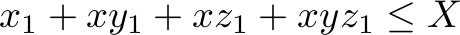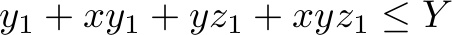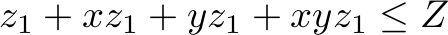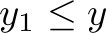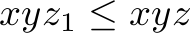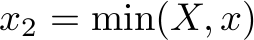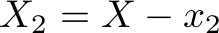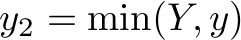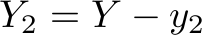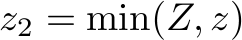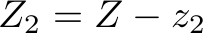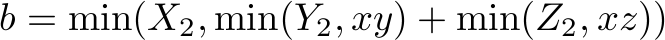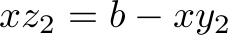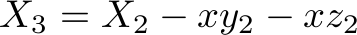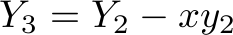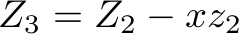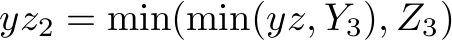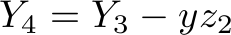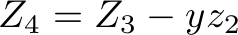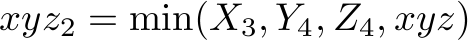Fulfilling Orders – An Algorithm Engineering Exercise
Recently, Zalando Software Engineering organized a hackathon on a website called hackerrank.com. The event was conveniently scheduled on a Saturday, and I decided to participate as I was curious. The problems that were to be solved in the hackathon were algorithmical, very well explained, and required to think about the nature of the problems in order to be solved correctly. All in all, taking part in the hackathon was a very nice experience, and I later used one of the problems as a challenge problem to exercise algorithm engineering with one of my PhD students. The problem is defined as follows:
Problem Definition:
We are organizing the shipping process in a company and have a set of orders on file. There are three different types of goods, let's name them 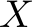 ,
, 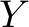 , and
, and 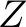 , and every customer can only order one item of every good type. So there are 7 different orders that a customer can make:
, and every customer can only order one item of every good type. So there are 7 different orders that a customer can make:
Ordering only an item of type
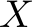
Ordering only an item of type
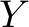
Ordering only an item of type
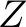
Ordering an item of type
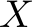 and one of type
and one of type 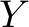
Ordering an item of type
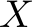 and one of type
and one of type 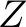
Ordering an item of type
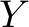 and one of type
and one of type 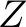
Ordering items of types
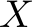 ,
, 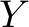 , and
, and 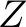 .
.
Let us use the variable names 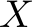 ,
, 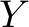 ,
, 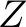 to denote how many items of each type our company has in stock, and let us use
to denote how many items of each type our company has in stock, and let us use 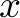 ,
, 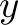 ,
, 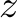 ,
,  ,
, 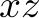 ,
, 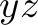 , and
, and 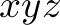 as variable names for denoting how many orders of each of the above types we have.
as variable names for denoting how many orders of each of the above types we have.
We want to find a subset of the orders whose number (cardinality) is as high as possible such that fulfilling them all does not exceed the number of items in stock.
We can formalize the problem by asking for some number of fulfilled orders 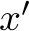 ,
, 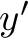 ,
, 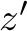 ,
, 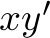 ,
, 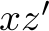 ,
, 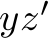 ,
, 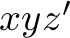 such that
such that
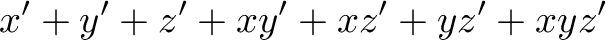
is as high as possible while satisfying the constraints
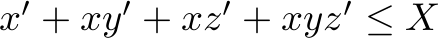 ,
,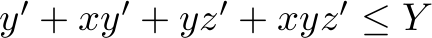 , and
, and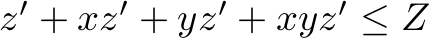 ,
,
which state that there is a limited supply of each good type, and the constraints
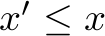 ,
,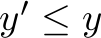 ,
,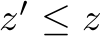 ,
,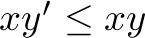 ,
,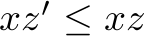 ,
,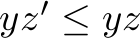 , and
, and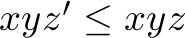 ,
,
which state that not more orders can be served than there are in the order book. All numbers are integer and non-negative.
Efficiency Requirements:
The solution (algorithm) should work with numbers in the 1000s and there is a computation time limit of 2 seconds (for solutions in C) or 10 seconds (for solutions in Python) on a moderately modern computer, so brute forcing all possible combinations of values 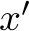 ,
, 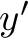 ,
, 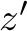 ,
, 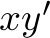 ,
, 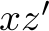 ,
, 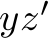 ,
, 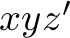 up to some sufficient bound (such as, e.g.,
up to some sufficient bound (such as, e.g., 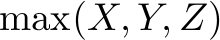 ) is infeasible.
) is infeasible.
A First Lazy Solution: Integer Linear Programming
The problem definition above looks quite simple: We are given 10 integer constants (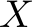 ,
, 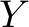 ,
, 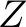 ,
, 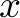 ,
, 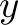 ,
, 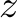 ,
,  ,
, 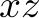 ,
, 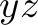 ,
, 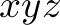 ) and we search for values for the integer variables
) and we search for values for the integer variables 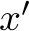 ,
, 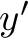 ,
, 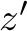 ,
, 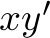 ,
, 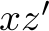 ,
, 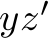 , and
, and 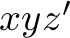 that maximize
that maximize 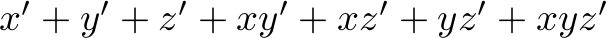 . Since all constraints listed above are linear and the optimization function is linear, we can model this problem as an integer linear program (ILP).
. Since all constraints listed above are linear and the optimization function is linear, we can model this problem as an integer linear program (ILP).
ILP solving is a classical technique in operations research and nowadays, off-the-shelf solvers are available to solve so-called linear programs. The word “program” in this context refers to a set of constraints on the solution and an optimization function, so there is nothing to be programmed in the software-engineering sense. For 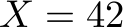 ,
, 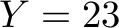 ,
, 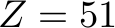 ,
, 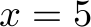 ,
, 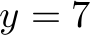 ,
, 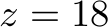 ,
, 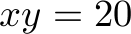 ,
, 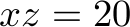 ,
, 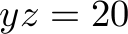 ,
, 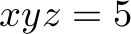 , such a linear program in the input format for the lp_solve tool looks as follows:
, such a linear program in the input format for the lp_solve tool looks as follows:
max: x+y+z+xy+xz+yz+xyz; x<=5; y<=7; z<=18; xy<=20; xz<=20; yz<=20; xyz<=5; x+xy+xz+xyz <= 42; y+xy+yz+xyz <= 23; z+xz+yz+xyz <= 51; int x; int y; int z; int xy; int xz; int yz; int xyz;
Note that the dashes of the variables names have been left out in the input file as the undashed variables do not appear named in the problem instance file. The lp_solve tool easily computes a solution in less than 10 ms on a moderately modern computer. The output of the tool looks as follows:
Value of objective function: 66.00000000 Actual values of the variables: x 5 y 7 z 18 xy 3 xz 20 yz 8 xyz 5
So in this example, 66 orders can be fulfilled.
Now we could say that we are done with solving the problem as the approach works reasonably fast, but using an ILP solver would defeat the purpose of the hackathon. So there should be a solution that is reasonably simple to implement using only language features and standard libraries of commonly used programming languages. It should also be noted that ILP solving is NP-complete, so there probably exists no fast algorithm for solving this problem. Since the number of variables and constraints is fixed, this is not a big concern, but the question remains if there is a more direct solution that also yields insights into the main properties of the problem. I expected this to be the case, as otherwise the problem would be an odd choice for a general-audience hackathon.
A First Analysis
Probably the first idea that comes into mind when trying to maximize the number of orders fulfilled is to execute them greedily. We order the variables 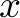 ,
, 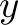 ,
, 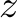 ,
,  ,
, 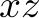 ,
, 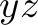 ,
, 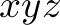 into a list and then iterate over the list. While doing so, we update
into a list and then iterate over the list. While doing so, we update 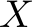 ,
, 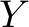 , and
, and 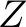 by executing as many orders of the respective order types as possible and subtracting the number of items used for doing so from
by executing as many orders of the respective order types as possible and subtracting the number of items used for doing so from 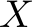 ,
, 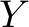 and
and 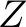 .
.
Example:
Let us try out this idea on an example. We fix the order 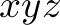 ,
,  ,
, 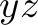 ,
, 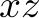 ,
, 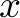 ,
, 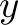 ,
, 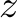 for
for 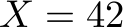 ,
, 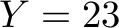 ,
, 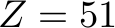 ,
, 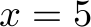 ,
, 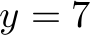 ,
, 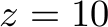 ,
, 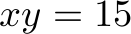 ,
, 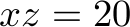 ,
, 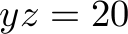 , and
, and 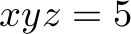 . The following table represents the variable values while the algorithm tries to fulfill as many orders as possible:
. The following table represents the variable values while the algorithm tries to fulfill as many orders as possible:
![text{ begin{tikzpicture} node[inner sep=4pt] (a) at (0,0) { begin{tabular}{l||l|l|l||l} textbf{Order type considered} & makemath{X} & makemath{Y} & makemath{Z} & textbf{Executed orders} hline hline - & 41 & 23 & 51 & - hline makemath{xyz} & 36 & 18 & 46 & makemath{xyz: 5} hline makemath{xy} & 21 & 3 & 46 & makemath{xy: 15} hline makemath{yz} & 21 & 0 & 43 & makemath{yz: 3} hline makemath{xz} & 1 & 0 & 23 & makemath{xz: 20} hline makemath{x} & 0 & 0 & 23 & makemath{x: 1} hline makemath{y} & 0 & 0 & 23 & makemath{y: 0} hline makemath{z} & 0 & 0 & 13 & makemath{z: 10} end{tabular} }; end{tikzpicture} }](eqs/hwz8nbjklh2dd-280.png)
The overall number of orders fulfilled in this example is 54. But is it optimal? We try ordering the orders differently – this time, we just use the reverse order compared to the previous table.
![text{ begin{tikzpicture} node[inner sep=4pt] (a) at (0,0) { begin{tabular}{l||l|l|l||l} textbf{Order type considered} & makemath{X} & makemath{Y} & makemath{Z} & textbf{Executed orders} hline hline - & 41 & 23 & 51 & - hline makemath{z} & 41 & 23 & 41 & makemath{z: 10} hline makemath{y} & 41 & 16 & 41 & makemath{y: 7} hline makemath{x} & 36 & 16 & 41 & makemath{x: 5} hline makemath{xz} & 16 & 16 & 21 & makemath{xz: 20} hline makemath{yz} & 16 & 0 & 5 & makemath{yz: 16} hline makemath{xy} & 16 & 0 & 5 & makemath{xy: 0} hline makemath{xyz} & 16 & 0 & 5 & makemath{xyz: 0} hline end{tabular} }; end{tikzpicture} }](eqs/puv233nfllzz-280.png)
This time, we computed a plan to serve 58 orders, which is more than before.
The example shows that when following the greedy approach, the order of the orders is important. But which one is the right one? Intuitively, larger orders should be processed last, as they drain the number of items in stock more than smaller orders, but both type of orders count in the same way towards the overall objective.
This line of thought can be completed by considering (for the example case of  and
and 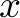 orders) that there is never a reason to prefer an
orders) that there is never a reason to prefer an  order over an
order over an 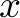 order – the latter requires a strictly smaller amount of resources, so whenever we have a solution for the fulfilled orders in which not all
order – the latter requires a strictly smaller amount of resources, so whenever we have a solution for the fulfilled orders in which not all 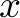 orders are fulfilled and some
orders are fulfilled and some  orders are fulfilled, then we can translate it to a solution in which one more
orders are fulfilled, then we can translate it to a solution in which one more 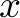 order is fulfilled at the cost of fulfilling fewer
order is fulfilled at the cost of fulfilling fewer  orders.
Similarly, the
orders.
Similarly, the 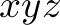 orders should only be fulfilled if the number of orders fulfilled of all other types has been maxed out, as fulfilling
orders should only be fulfilled if the number of orders fulfilled of all other types has been maxed out, as fulfilling 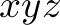 orders is strictly more expensive than fulfilling any other order.
So the second order in the example above is not bad. The
orders is strictly more expensive than fulfilling any other order.
So the second order in the example above is not bad. The 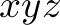 orders are checked last and the order of the first three order types does not matter, as the
orders are checked last and the order of the first three order types does not matter, as the 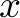 ,
, 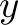 and
and 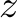 orders are independent.
The only thing that is not obvious is in which order to fulfill the
orders are independent.
The only thing that is not obvious is in which order to fulfill the  ,
, 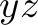 , and
, and 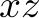 orders.
orders.
Since there are only three different orders of 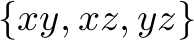 , it is quite simple to try out all orders of them. So we would run the greedy algorithm for the orders
, it is quite simple to try out all orders of them. So we would run the greedy algorithm for the orders
and just pick the best possible solution that we find with any of these orders. If a greedy approach is correct, then one of them will yield the best solution.
Putting this idea into an algorithm implementation is quite simple, and for the said hackathon this is the solution that I submitted. The hackerrank.com website gave me full credit for the solution as it works correctly on all test cases on which it was checked. While I wasn't entirely sure whether the solution is really a good one, at the point, I moved on to the other problems in the competition, as it required me to be as fast as possible with solving all problems (and I was not done at that point). After the competition, I checked which solution the winner of the competition had (which seems to be possible if you submitted a solution getting you 100% of the points). It was essentially the same, except that it was written in C++ (while I wrote mine in Python).
After I gave this problem to my PhD student and he came with the same solution, I however requested him to prepare a correctness proof of this idea, as it is not at all obvious whether this solution is really correct. As it turns out, that is because it actually isn't correct.
A More Balanced Use of Resources
To see the problem with the approach above, let us consider an example with only two-item orders (as we have already found out that they are the ones for which a trade-off may need to be made).
Example:
Let us have 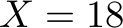 ,
, 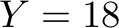 ,
, 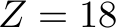 ,
, 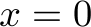 ,
, 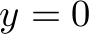 ,
, 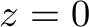 ,
, 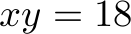 ,
, 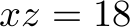 ,
, 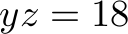 ,
, 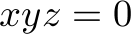 . Due to the symmetry of the example, we only need to consider one ordering of the order types, which, without loss of generality, we choose to be
. Due to the symmetry of the example, we only need to consider one ordering of the order types, which, without loss of generality, we choose to be 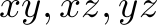 .
.
![text{ begin{tikzpicture} node[inner sep=4pt] (a) at (0,0) { begin{tabular}{l||l|l|l||l} textbf{Order type considered} & makemath{X} & makemath{Y} & makemath{Z} & textbf{Executed orders} hline hline - & 18 & 18 & 18 & - hline makemath{xy} & 0 & 0 & 18 & makemath{xy: 18} hline makemath{xz} & 0 & 0 & 18 & makemath{yz: 0} hline makemath{yz} & 0 & 0 & 18 & makemath{xy: 0} end{tabular} }; end{tikzpicture} }](eqs/9qkb42lgfjhb-280.png)
Using the algorithm from above, we thus fulfill all orders of one type and keep the others untouched. Overall, 18 orders are fulfilled. This is less than optimal, as we can also execute 9 orders of each type, which leads to an empty stock and 27 orders having been fulfilled.
So what still seems to be missing is the idea to balance the consumption of the items such that the greediness does not keep us from fulfilling later order types in the order type list. But when is that the case?
An idea is to plan two order types greedily at a time. If for example for the  and
and 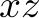 order types, we can fulfill
order types, we can fulfill 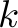 of such orders in total, we may want to balance these
of such orders in total, we may want to balance these 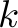 orders between
orders between  and
and 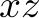 types in a way that maximizes
types in a way that maximizes 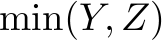 afterwards, as this leaves as many resources for the
afterwards, as this leaves as many resources for the 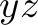 order type as possible. But we can still try to maximize
order type as possible. But we can still try to maximize 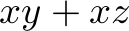 first, as unnecessarily leaving an
first, as unnecessarily leaving an 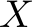 item in stock cannot make a solution better.
item in stock cannot make a solution better.
Now how many orders of types  and
and 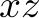 can we fulfill? We can fulfill at most
can we fulfill? We can fulfill at most 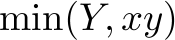 most orders of type
most orders of type  and at most
and at most 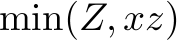 types of type
types of type 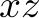 , and we can never fulfill more orders of types
, and we can never fulfill more orders of types  and
and 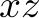 together than
together than 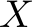 . Together, this gives us
. Together, this gives us 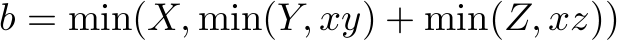 many orders of
many orders of  and
and 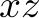 . Now, we need to balance the ones of types
. Now, we need to balance the ones of types  and
and 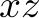 to be fulfilled. Let
to be fulfilled. Let 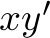 be the number of
be the number of  orders fulfilled. We want to maximize
orders fulfilled. We want to maximize
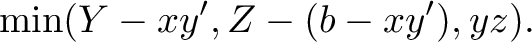
Choosing 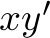 such that
such that 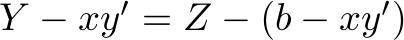 is the best way to maximize this expression (as
is the best way to maximize this expression (as 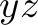 is constant), so we compute:
is constant), so we compute:
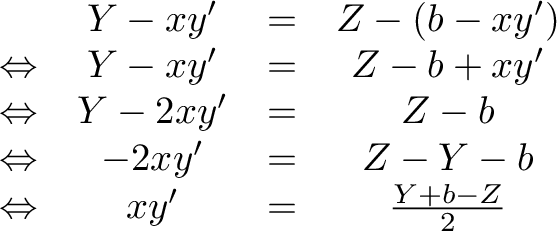
At the same time 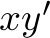 is bounded from below by
is bounded from below by 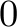 and from above by
and from above by  , so
, so 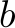 should be truncated accordingly when using the equation above. In case
should be truncated accordingly when using the equation above. In case 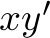 is non-integer, this means that after fulfilling the
is non-integer, this means that after fulfilling the  and
and 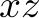 orders, one of the numbers of remaining
orders, one of the numbers of remaining 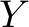 and
and 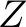 items has to be odd. In this case, whether
items has to be odd. In this case, whether 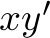 is rounded up or down should intuitively not matter, but we should verify this intuition somehow.
is rounded up or down should intuitively not matter, but we should verify this intuition somehow.
We are now ready to give a solution program (in Python 3):
import sys import math # Read the input problem (X,Y,Z) = [int(a) for a in sys.stdin.readline().strip().split(" ")] nofOrders = int(sys.stdin.readline().strip()) orders = {(0,0,1):0,(0,1,0):0,(1,0,0):0,(0,1,1):0,(1,0,1):0,(1,1,0):0,(1,1,1):0} for i in range(0,nofOrders): data = sys.stdin.readline().strip().split(",") thisTuple = [0,0,0] for a in data: if a=="A": thisTuple[0] += 1 elif a=="B": thisTuple[1] += 1 elif a=="C": thisTuple[2] += 1 else: print("'"+a+"'") assert False orders[tuple(thisTuple)]+= 1 # Get the values into the variables x = orders[(1,0,0)] y = orders[(0,1,0)] z = orders[(0,0,1)] xy = orders[(1,1,0)] xz = orders[(1,0,1)] yz = orders[(0,1,1)] xyz = orders[(1,1,1)] # Serve single items totalNofOrders = 0 totalNofOrders += min(X,x) X -= min(X,x) totalNofOrders += min(Y,y) Y -= min(Y,y) totalNofOrders += min(Z,z) Z -= min(Z,z) # Two-item orders b = min(X,min(Y,xy)+min(Z,xz)) xyf = (Y + b - Z) // 2 xyf = max(0,min([xy,xyf,b])) totalNofOrders += b X -= xyf Y -= xyf X -= (b - xyf) Z -= (b - xyf) yzf = min(min(yz,Y),Z) totalNofOrders += yzf Y -= yzf Z -= yzf # Three-item orders totalNofOrders += min([X,Y,Z,xyz]) # Print result print(totalNofOrders)
The first couple of lines read the input problem in the format described on the hackerrank.com problem page. To simplify reading the code, they are then copied to variables with the same names as in the equations above. Then, the number of fulfillable orders is computed and the program prints out this number. In the original problem description on hackerrank.com, this was the only expected output, so the program does not do more than that. Note that the variable xyf represents the number of  orders fulfilled.
orders fulfilled.
Funnily, this program only fulfills 14 of the 17 test cases on hackerrank.com. Looking at the example, we can see that the program prints higher numbers of fulfilled orders than expected. This is not surprising, as we possibly gave a strictly better solution than the one accepted by the website. But again we should verify that the program is really correct rather than assuming that because the test cases on hackerrank.com accept a sub-optimal solution, it is OK for our (hopefully) correct program not to satisfy all test cases.
So the main question is now if we found a correct solution. The explanation above gives some intuition on why one may believe this computation to be correct, but perhaps we are overlooking something? We could now prepare a formal mathematical proof (where we may still make some errors), but for this program, there is an easier way to check the solution for correctness.
Verifying the solution
The algorithmic main part of the program above is actually quite simple: it only performs a few basic calculations on the variables 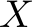 ,
, 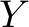 ,
, 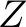 ,
, 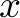 ,
, 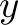 ,
, 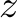 ,
,  ,
, 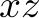 ,
, 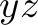 , and
, and 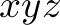 , and the program does not have any loops. The difficulty in program verification is typically to find suitable loop invariants, but since we do not have any in this example, we can use an SMT solver to check the program for correctness.
, and the program does not have any loops. The difficulty in program verification is typically to find suitable loop invariants, but since we do not have any in this example, we can use an SMT solver to check the program for correctness.
In an input instance to an SMT solver, we ask for a valuation of some variables such that certain requirements that we can express in a closed form are fulfilled. In this regard, SMT solving is similar to integer linear program (as we used above), but more flexible in what can be modeled. This flexibility comes at a computational price, but the use of the 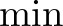 function makes it appear as if the added expressivity would be helpful. Why exactly this is the case is unfortunately beyond the scope of this document, so let us just assume that an SMT solver is a rational choice for verifying our solution.
function makes it appear as if the added expressivity would be helpful. Why exactly this is the case is unfortunately beyond the scope of this document, so let us just assume that an SMT solver is a rational choice for verifying our solution.
But what is it that we are searching for? We want to see if there are some values for 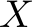 ,
, 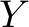 ,
, 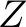 ,
, 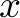 ,
, 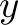 ,
, 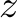 ,
,  ,
, 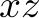 ,
, 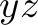 , and
, and 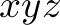 for which the program above computes a sub-optimal solution. A solution has this property if there is a better solution. Since in SMT solving, the variables can have all values that fulfill all constraints, we start by stating the properties that the other solution should have. Let us use the variables
for which the program above computes a sub-optimal solution. A solution has this property if there is a better solution. Since in SMT solving, the variables can have all values that fulfill all constraints, we start by stating the properties that the other solution should have. Let us use the variables 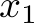 ,
, 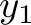 ,
, 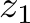 ,
, 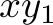 ,
, 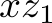 ,
, 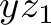 , and
, and 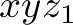 to model the number of fulfilled orders in the optimal (or at least better) solution. We have the following constraints on them:
to model the number of fulfilled orders in the optimal (or at least better) solution. We have the following constraints on them:
Now we need to define how the algorithm above behaves. As SMT instances model mathematical problems, there is no concept of reassignment for variables. Thus, whenever in the program a variable value is overwritten, we need to use a fresh variable to define the new value in the program from that point onwards. Let us use the variables 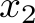 ,
, 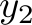 ,
, 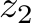 ,
, 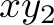 ,
, 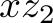 ,
, 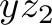 , and
, and 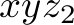 to model the number of fulfilled orders in the solution computed by the program above. We have the following constraints:
to model the number of fulfilled orders in the solution computed by the program above. We have the following constraints:
Finally, we need the constraint that the optimal solution is better than the one computed with the algorithm:
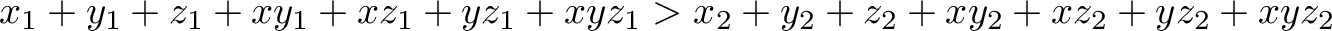
We can now build an SMT instance that captures all of these constraints. We refer to the Tutorial of the SMT solver Z3 for a description of the syntax of the input files, and move straight to the solution.
(declare-const x Int) (declare-const y Int) (declare-const z Int) (declare-const xy Int) (declare-const xz Int) (declare-const yz Int) (declare-const xyz Int) (declare-const x1 Int) (declare-const y1 Int) (declare-const z1 Int) (declare-const xy1 Int) (declare-const xz1 Int) (declare-const yz1 Int) (declare-const xyz1 Int) (declare-const x2 Int) (declare-const y2 Int) (declare-const z2 Int) (declare-const xy2 Int) (declare-const xz2 Int) (declare-const yz2 Int) (declare-const xyz2 Int) (declare-const X Int) (declare-const Y Int) (declare-const Z Int) (assert (>= x 0)) (assert (>= y 0)) (assert (>= z 0)) (assert (>= xy 0)) (assert (>= xz 0)) (assert (>= yz 0)) (assert (>= xyz 0)) (assert (>= x1 0)) (assert (>= y1 0)) (assert (>= z1 0)) (assert (>= xy1 0)) (assert (>= xz1 0)) (assert (>= yz1 0)) (assert (>= xyz1 0)) (assert (>= X 0)) (assert (>= Y 0)) (assert (>= Z 0)) (define-fun min2 ((a Int) (b Int)) Int (ite (< a b) a b)) (define-fun max2 ((a Int) (b Int)) Int (ite (> a b) a b)) (assert (<= (+ x1 xy1 xz1 xyz1) X)) (assert (<= (+ y1 xy1 yz1 xyz1) Y)) (assert (<= (+ z1 xz1 yz1 xyz1) Z)) (assert (<= x1 x)) (assert (<= y1 y)) (assert (<= z1 z)) (assert (<= xy1 xy)) (assert (<= xz1 xz)) (assert (<= yz1 yz)) (assert (<= xyz1 xyz)) (assert (= x2 (min2 X x))) (declare-const X2 Int) (assert (= X2 (- X x2))) (assert (= y2 (min2 Y y))) (declare-const Y2 Int) (assert (= Y2 (- Y y2))) (assert (= z2 (min2 Z z))) (declare-const Z2 Int) (assert (= Z2 (- Z z2))) (declare-const b Int) (assert (= b (min2 X2 (+ (min2 Y2 xy) (min2 Z2 xz))))) (assert (= xy2 (max2 0 (min2 xy (min2 b (div (- (+ Y2 b) Z2) 2)))))) (assert (= xz2 (- b xy2))) (declare-const X3 Int) (assert (= X3 (- (- X2 xy2) xz2))) (declare-const Y3 Int) (assert (= Y3 (- Y2 xy2))) (declare-const Z3 Int) (assert (= Z3 (- Z2 xz2))) (assert (= yz2 (min2 (min2 yz Y3) Z3))) (declare-const Y4 Int) (assert (= Y4 (- Y3 yz2))) (declare-const Z4 Int) (assert (= Z4 (- Z3 yz2))) (assert (= xyz2 (min2 X3 (min2 Y4 (min2 Z4 xyz))))) (assert (< (+ x2 y2 z2 xy2 xz2 yz2 xyz2) (+ x1 y1 z1 xy1 xz1 yz1 xyz1))) (check-sat)
Most of the lines are concerned with declaring variables, ensuring that all variables whose values are not computed by our algorithm are all non-negative, and defining the behavior of the algorithm.
The SMT solver z3 by Microsoft Research returns quickly ( seconds on a moderately modern PC) that there is no assignment to the variables that satisfies all constraints. So unless a modeling error has been made, the program above never returns sub-optimal solutions.
seconds on a moderately modern PC) that there is no assignment to the variables that satisfies all constraints. So unless a modeling error has been made, the program above never returns sub-optimal solutions.
Now that we know that the program does not miss optima, the question arises whether perhaps there is still another bug lurking somewhere in the code, e.g., because the algorithm returns incorrect solutions. We can use z3 again to find it. What we want to obtain is an input to the algorithm such that the solution is not correct. We already established correctness conditions for the reference solution in the SMT instance above, and modify the last assert statement of the instance to allow variable valuations for which either the solution computed by the algorithm above is suboptimal or incorrect. Since the correctness condition consists of many conjuncts, it suffices if just one of the is violated. We replace the last assert statement in the above code by:
(assert (or
(< (+ x2 y2 z2 xy2 xz2 yz2 xyz2) (+ x1 y1 z1 xy1 xz1 yz1 xyz1))
(< x2 0)
(< y2 0)
(< z2 0)
(< xy2 0)
(< xz2 0)
(< yz2 0)
(< xyz2 0)
(> (+ x2 xy2 xz2 xyz2) X)
(> (+ y2 xy2 yz2 xyz2) Y)
(> (+ z2 xz2 yz2 xyz2) Z)
(> x2 x)
(> y2 y)
(> z2 z)
(> xy2 xy)
(> xz2 xz)
(> yz2 yz)
(> xyz2 xyz)
))
This time, z3 computes a sat result, so there may be a case where the program behaves incorrectly. After adding the line (get-model) to the SMT instance and running z3 again, we obtain the following output:
sat
(model
(define-fun X2 () Int
4)
(define-fun z1 () Int
0)
(define-fun xyz () Int
0)
(define-fun Y4 () Int
1)
(define-fun x2 () Int
1)
(define-fun xyz1 () Int
0)
(define-fun xy1 () Int
3)
(define-fun yz () Int
1)
(define-fun z2 () Int
0)
(define-fun Y () Int
5)
(define-fun xy2 () Int
2)
(define-fun xy () Int
3)
(define-fun yz2 () Int
0)
(define-fun z () Int
0)
(define-fun xz2 () Int
2)
(define-fun Y2 () Int
3)
(define-fun y2 () Int
2)
(define-fun y1 () Int
0)
(define-fun y () Int
2)
(define-fun xyz2 () Int
0)
(define-fun xz () Int
1)
(define-fun x1 () Int
0)
(define-fun yz1 () Int
0)
(define-fun xz1 () Int
1)
(define-fun X () Int
5)
(define-fun b () Int
4)
(define-fun Y3 () Int
1)
(define-fun Z () Int
2)
(define-fun X3 () Int
0)
(define-fun Z4 () Int
0)
(define-fun x () Int
1)
(define-fun Z2 () Int
2)
(define-fun Z3 () Int
0)
)
This output format is cumbersome to read, so let us rearrange it. The input to the algorithm is:
![text{ begin{tikzpicture} node[inner sep=4pt] (a) at (0,0) { begin{tabular}{l|l|l||l|l|l|l|l|l|l} makemath{X} & makemath{Y} & makemath{Z} & makemath{x} & makemath{y} & makemath{z} & makemath{xy} & makemath{xz} & makemath{yz} & makemath{xyz} hline 5 & 5 & 2 & 1 & 2 & 0 & 3 & 1 & 1 & 0 end{tabular} }; end{tikzpicture} }](eqs/b0xg8w6r4u6y-280.png)
The reference solution generated by the SMT solver is:
![text{ begin{tikzpicture} node[inner sep=4pt] (a) at (0,0) { begin{tabular}{l|l|l|l|l|l|l} makemath{x_1} & makemath{y_1} & makemath{z_1} & makemath{xy_1} & makemath{xz_1} & makemath{yz_1} & makemath{xyz_1} hline 0 & 0 & 0 & 3 & 1 & 0 & 0 end{tabular} }; end{tikzpicture} }](eqs/feauqzg7pgxjb-280.png)
We can see that this is suboptimal as it leaves one-item orders unfulfilled even though there is enough stock to fulfill at least one more of them. The solution that – according to the SMT instance – our implementation generated is:
![text{ begin{tikzpicture} node[inner sep=4pt] (a) at (0,0) { begin{tabular}{l|l|l|l|l|l|l} makemath{x_2} & makemath{y_2} & makemath{z_2} & makemath{xy_2} & makemath{xz_2} & makemath{yz_2} & makemath{xyz_2} hline 1 & 2 & 0 & 2 & 2 & 0 & 0 end{tabular} }; end{tikzpicture} }](eqs/h4r12aooq7uad-280.png)
The problem seems to be that our implementation produces a solution in which more 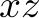 orders are fulfilled than there are available. We need to distinguish the cases that the SMT instance was written down incorrectly and the case that the Python code above is actually wrong. So we generate the test case found by the SMT solver as an input to the Python program using the format described in the hackerrank.com problem description. It looks as follows:
orders are fulfilled than there are available. We need to distinguish the cases that the SMT instance was written down incorrectly and the case that the Python code above is actually wrong. So we generate the test case found by the SMT solver as an input to the Python program using the format described in the hackerrank.com problem description. It looks as follows:
5 5 2 8 A B B A,B A,B A,B A,C B,C
Note that the last few lines represent the orders, and on the original problem page, the items are called A, B, and C rather than 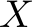 ,
, 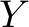 , and
, and 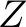 as we used as item names here.
Running the program (with some additional code lines to output the numbers of fulfilled orders) shows that the program computes exactly the (non-)solution that the SMT solver found. So the program is indeed working incorrectly, and we actually found the bug using an SMT solver. Not bad at all.
as we used as item names here.
Running the program (with some additional code lines to output the numbers of fulfilled orders) shows that the program computes exactly the (non-)solution that the SMT solver found. So the program is indeed working incorrectly, and we actually found the bug using an SMT solver. Not bad at all.
Fixing the Bug
What seems to be the problem with the first version of the code is that variable 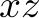 is not looked at when deciding how many orders of types
is not looked at when deciding how many orders of types  and
and 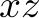 to fulfill. The number of
to fulfill. The number of 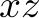 orders to fulfill is actually
orders to fulfill is actually 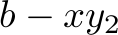 in the equations above, so
in the equations above, so 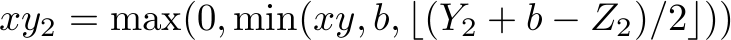 should not be too low to make sense of this idea. We can see that the problem seems to be that we need
should not be too low to make sense of this idea. We can see that the problem seems to be that we need 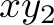 to be high enough to have
to be high enough to have 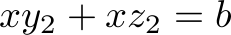 . So we modify this equation to:
. So we modify this equation to:
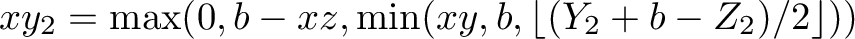
To incorporate this idea into the SMT instance, we change the line
(assert (= xy2 (max2 0 (min2 xy (min2 b (div (- (+ Y2 b) Z2) 2))))))
to
(assert (= xy2 (max2 (- b xz) (max2 0 (min2 xy (min2 b (div (- (+ Y2 b) Z2) 2)))))))
Running Z3 again yields that there is indeed no model for this SMT instance (which you can download here). We only need to fix a single line in the Python code to incorporate this change. Running the program (which you can download here) on the test case above yields:
![text{ begin{tikzpicture} node[inner sep=4pt] (a) at (0,0) { begin{tabular}{l|l|l|l|l|l|l} makemath{x_2} & makemath{y_2} & makemath{z_2} & makemath{xy_2} & makemath{xz_2} & makemath{yz_2} & makemath{xyz_2} hline 1 & 2 & 0 & 3 & 1 & 0 & 0 end{tabular} }; end{tikzpicture} }](eqs/kt2bi5h3yvk9c-280.png)
This solution makes much more sense.
Finally, we want to see if the new program makes more test cases on hackerrank.com pass. After all, we have evidence that the SMT instance and the Python program coincide (as they both exhibited the same bug), and the result by the SMT solver suggests that the program is now correct. There can always be some more modeling errors in the SMT instance, but the fact that we found a bug with it should give us some level of confidence.
The new program (with the additional output lines for 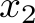 ,
, 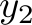 ,
, 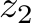 ,
,  removed because the tester does not expect such output) makes all of the test cases pass. We can conclude with the observation that indeed all of the test cases on the website are correct (and hence the fact that our earlier solution failed three test cases was due to the bug in our program). Yet, the set of test cases was incomplete, as the website accepted solution programs that did not find the optimal number of fulfilled orders for an example that we discussed above.
removed because the tester does not expect such output) makes all of the test cases pass. We can conclude with the observation that indeed all of the test cases on the website are correct (and hence the fact that our earlier solution failed three test cases was due to the bug in our program). Yet, the set of test cases was incomplete, as the website accepted solution programs that did not find the optimal number of fulfilled orders for an example that we discussed above.
Finally, we want to check if it mattered whether we were rounding up or down in the program when dividing by two. We do this straight on the SMT instance and modify the line
(assert (= xy2 (max2 (- b xz) (max2 0 (min2 xy (min2 b (div (- (+ Y2 b) Z2) 2)))))))
to
(define-fun divUp ((a Int) (b Int)) Int (ite (= (* (div a b) b) a) (div a b) (+ (div a b) 1) )) (assert (= xy2 (max2 (- b xz) (max2 0 (min2 xy (min2 b (divUp (- (+ Y2 b) Z2) 2)))))))
This snippet defines a division function that rounds up and uses it in a modified constraint. Running z3 on the modified input file yields that the SMT instance is still unsatisfiable, so indeed our assumption that whether we round up or down for the division by two in our algorithm makes no difference is correct.