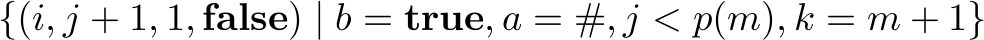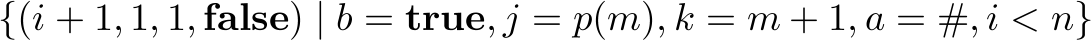Author's notes on the paper “Short Witnesses and Accepting Lassos in Omega-automata”

Erratum

On page 9 of the paper (page 269 of the proceedings), there is a small error in the index bounds in the description of the safety automaton. The second and third bullet points in the definition of the transition function should read:

Relationship to Other Work

The paper discusses finding short accepting witnesses and lassos in omega-automata. As these can be seen as special cases of two-player games with omega-regular winning objectives, the results have some important implications for the synthesis of finite-state systems: finding a system implementation with as few states as possible satisfying the specification encoded into the game graph is a tough task: it is NP-hard to approximate within any polynomial.

The proof idea of Theorem 6 has been used independently in the paper Equivalence and Inclusion Problem for Strongly Unambiguous Büchi Automata by Nicolas Bousquet und Christof Löding, also published at LATA 2010.

Slides

The slides of the talk given at LATA 2010 are available here.